Imagine you’re knitting a scarf. You’re several rows in when you accidentally miss a stitch. At first, it doesn’t seem like a big deal. The pattern looks mostly intact, and there’s no immediate sign of trouble.

Now, let’s apply this to maths. Picture a student, Josh, who is 12 years old and learning fractions. Josh misunderstands how fractions work—specifically, they think you add fractions by adding both the numerators and denominators straight across. Just like that missed stitch, this misconception doesn’t immediately cause issues with simpler maths problems.
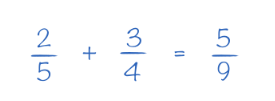
Path 1: Fixing the Missed Stitch Early
A few rows later, the missed stitch starts to stand out. The fabric doesn’t lie as flat, and the pattern doesn’t look quite right. You notice the error and stop to investigate. It takes a bit of work, maybe even a bit of unravelling, but you go back, catch the missed stitch, and correct it. From there, you can continue knitting, confident that your scarf will look just as it should, with no weak spots to worry about later.
For Josh, this would mean noticing their maths error a few months later, when fractions start to seem inconsistent and difficult. Maybe their teacher spots the pattern of mistakes or Josh realizes something isn’t adding up. They ask for help, correct the misconception, and move forward with a solid understanding. Now, just like the corrected knitting row, they’re ready to keep learning with confidence, building a strong foundation for more advanced concepts.
Path 2: Ignoring the Missed Stitch
But what if you ignore that missed stitch? You think it’s “just one stitch,” so you keep knitting. At first, it’s barely noticeable, but as you go further, the problem grows. The rows above start to pull and gap, making the fabric uneven, and you’re finding it harder to keep the pattern straight. The more you knit, the worse it gets, as each new row is affected by that one missed stitch. Now, even if you manage to finish the scarf, it’s at risk of coming undone. That small missed stitch has become a structural weakness, making the scarf less durable and more likely to tear with use.
This is what happens when Josh decides to “push through” with the fraction misconception, thinking it’s not worth going back to fix just yet. As they move into more advanced topics, the misconception grows, affecting related concepts like algebra and percentages. By the time they reach their GCSEs, their understanding is riddled with gaps, much like a scarf with a loose, vulnerable row running through it. Fixing it at this point would mean going back through years of learning—unravelling each layer of confusion and rebuilding from that original mistake. And just like fixing rows of knitting, it’s time-consuming and stressful, especially with the pressure of exams approaching. Alternatively, with the time constraint due to the hard deadline of the GCSE exams, you may need to settle for patching up the gaps with a handy trick or two. This can get you through your exams, but has only superficially fixed the problem - the structural weakness is still there underneath the patches. This leaves you with a lack of confidence going into adult life, and a shaky, unreliable understanding of maths.
The Takeaway: Catch Errors Early
Knitting a strong, resilient fabric requires fixing missed stitches as soon as they appear. Maths learning is the same way. Small misconceptions can seem minor at first, but the more you build on them, the more fragile and complex the problem becomes. Going back to fix the foundation early is always easier and quicker than unravelling rows of progress later. It is also more long-lasting and durable than relying on tricks to patch up misconceptions at a later point.
Whether in knitting or in maths, noticing and correcting mistakes early is the key to creating something strong, consistent, and dependable. That one small correction makes all the difference in the final result—leaving you with a fabric (or a foundation of knowledge) that won’t unravel under pressure.

Comments